Last month, it was reported that Chinese scientist He Jiankui had carried out the first human germline modification experiments using the CRISPR/Cas9 system. The procedure apparently resulted in the birth of twin girls (Lulu and Nana), each with modifications to the CCR5 gene. The supposed medical justification for this procedure is that there is a naturally segregating large scale deletion within CCR5 (known as Δ32), and individuals homozygous for this mutation are resistant to infection by certain forms of HIV. This justification simply does not hold water, and the procedure is an ethical trainwreck by any measure. Much has been written already about this already, and I'll refer readers elsewhere for commentary in this vein (e.g. here, here and here for a few examples).
One of the many things that makes He's actions so ethically and morally dubious is that neither child's genotype was actually modified to be homozygous for the Δ32 mutation. Instead, from what I've been able to gather, Lulu seems to be heterozygous (or perhaps mosaic?) for a 15 base pair in-frame deletion close to where the Δ32 mutation is located, while Nana appears to have a mosaic genotype, with some cells carrying a 1 base pair insertion, and others carrying a 4 base pair deletion, again, generally in the same region. None of these three mutations have been studied extensively, either in humans, or in a model system, meaning we really have no idea what they will do. The procedure should not have been done.
I was curious, however, after reading the following exchange on twitter, about whether we would expect that these mutations are truly "new", or if we might expect that there are other carriers already out there in the human population somewhere.
Why would you rule out the possibility that this particular mutation has arisen spontaneously? (I’m not suggesting that this would mean it’s harmless!) https://t.co/CSRxADGC2H
— Carl Zimmer (@carlzimmer) December 2, 2018
Of course, as Zimmer notes, the answer to this question has no bearing on the wisdom of the experiments, but I think it's an interesting question nonetheless.
There about 7.6 billion people alive on planet Earth right now, and each of them carries a handful of new mutations not present in their parents, so this makes for an obvious place to start: Are any of these mutations likely to be carried as de novo mutations not found in either of their parents?
To answer this question, we need to know two things. The first is the total number of opportunities that each of these mutations had to happen. As stated above, there are about 7.6 billion people on the planet, and because each is diploid, there should be about 15.2 billion chances for each of these mutations to occur. The second thing we need is the per site per generation mutation rate for each type of mutation. The best estimate I could find for insertion and deletion (indel) mutation rates was this 2016 paper from Besenbacher and coauthors. They report that the per position per generation probability of an indel mutation of any length is about 9.29*10-10. This estimate is based on an observation of 1282 indel mutations out of all of the callable sites they identified. Eyeballing their Figure S1, it looks like they observed about 5 fifteen base pair deletions, about 120 four base pair deletions, and about 250 one base pair insertions, meaning that roughly 3.9%, 9.3%, and 19.5% of all indels observed fell into these respective classes. We can use these figures to adjust the total indel rate downward, yielding estimated genome wide average rates of about 3.6*10-12, 8.7*10-11, and 1.8*10-10 respectively for the three different kinds of mutations. The confidence intervals on these estimates are likely pretty large, as they are each based on a relatively small amount of data, but we're just looking for ballpark estimates here, so these will do.
Assuming that mutation rates at this position are equal to the genome-wide average, we can find the expected number of copies of each mutation to have arisen as a de novo variant in a currently living individual simply by multiplying the mutation rate estimates times the population size times 2 (because of diploidy), yielding expected counts of: 0.054, 1.32 and 2.74, respectively. To find the probability that no living individual experienced one of these de novo mutations, we take negative exponential of this expected value (this is based on the assumption that the number of mutations follow a Poisson distribution), and the probabilities that at least one individual carries any of these specific mutations as a de novo is just one minus this value, yielding estimates of 0.055, 0.733 and 0.935, respectively.
So the one base pair deletion is highly likely, but not certain, to have arisen in a present day individual, while the four base pair deletion is less certain, and the 15 base pair deletion is unlikely but not impossible. This is simply a consequence of the fact that there are an enormous number of people alive today. Every possible mutation is exceedingly unlikely to happen, but given just over 15 billion opportunities, unlikely things can become probable.
Answering the question "Is there definitely at least one individual who carries this mutation, whether as a de novo mutation or inherited variant?" is more difficult. It helps however to realize that vast majority of segregating mutations are present at very low frequencies and occurred within the last handful of generations, simply because the majority of mutations are lost from the population due to drift relatively quickly. Only a very small proportion of all mutations every reach appreciable frequency. This means that we can try to get a handle on the answer to the above question by asking a slightly different question: "What is the probability that at least one individual carries a copy of the mutation that arose within the last X generations?" where X is on the order of dozens.
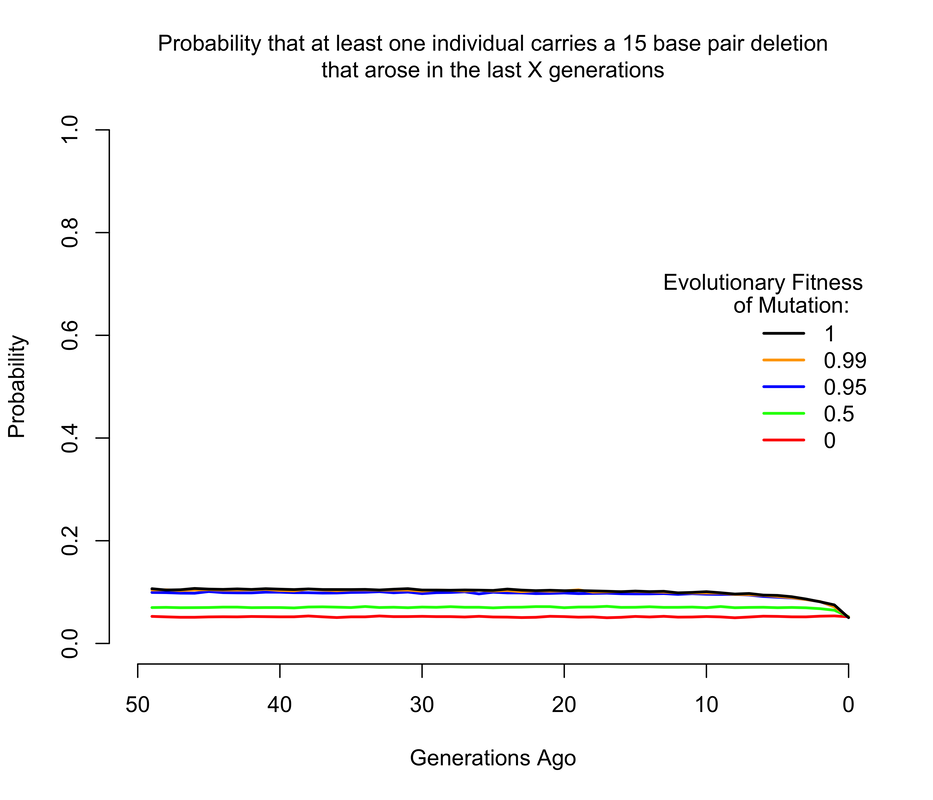
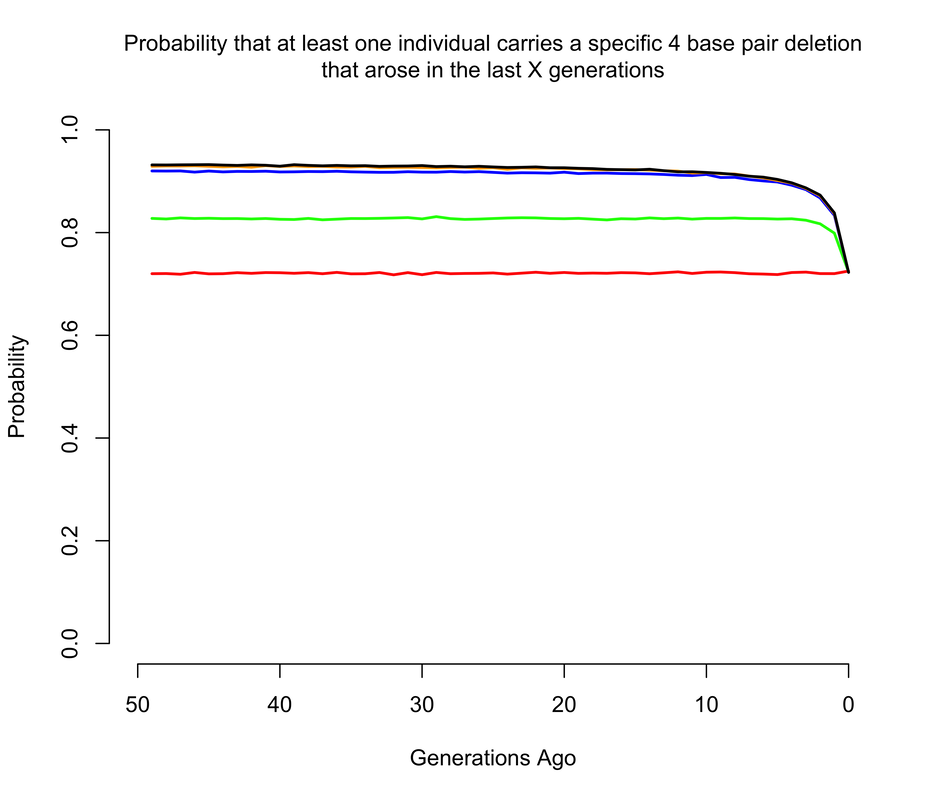
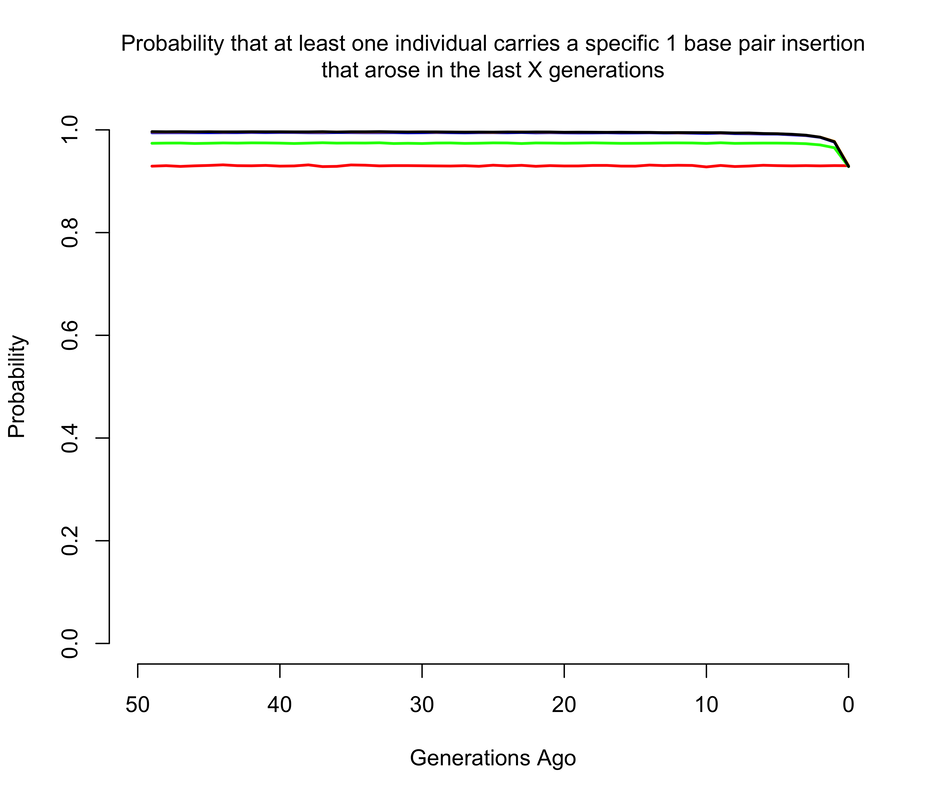
To get an approximate answer to this question, I wrote a simple branching process simulation. A branching process can be justified by noting that we're now only concerned with very recent mutations, and so we can ignore all demography except for total population size changes. Within the branching process framework, I approximated changes in population size by modeling the human population as having discrete, non-overlapping generations1. In the figures below, I show the probability that there is at least 1 copy of the mutation present in a living individual that arose within the last X generations, where X ranges from 0 to 50. Of course, I'm discussing all of this in the context of mutations of unknown consequence that were intentionally introduced into a human being, and it's worth noting that the consequences of the mutation(s) actually impact the answer. If any of the mutations have evolutionary fitness consequences (which may or may not coincide with medical consequences in a modern setting), then any mutation which occurred in a previous generation is less likely to have been passed down through the generations to the present day. It turns out that using a branching process also makes it relatively easy to incorporate the effects of selection, and I show results for a range of fitness costs. In this case, I am implicitly assuming that selection acts on individual fertility in heterozygotes2.
The results largely mirror those for the de novo mutations, with slightly higher probabilities when we allow that the mutations may have arisen more than a handful of generations ago, so long as they are not too costly in terms of fitness. For example, the 1 base pair insertion is certain to be present in the population unless it has a strong fitness cost, simply because if by chance it didn't arise as a de novo in the current generation, there's a pretty good chance it arose in one of the last few generations and then survived to the present day. The 4 base pair deletion is slightly less likely to be present, but still much more likely than not, while the the 15 base pair deletion has a smallish but definitely non-zero chance of being present.
Of course, I've made a number of approximations along the way here. For example, my mutation rate estimates are based on eyeballing a supplemental figure and the way I've dealt changes is population size (described below) is a pretty obvious kludge. I've also assumed that the mutation rates at this particular position are equal to my eye-balled estimate of the genome-wide average. Our understanding of mutation rates for insertions and deletions is in sufficiently early days that this is really the best I can do at the moment, but we know that point mutation rates vary depending on the surrounding context, and there's no reason to think this isn't true for indels too. So that's another layer of approximation. However, it does suggest that it's not too unlikely that there are individuals out there who carry copies of these mutations.
It's also worth noting just how quickly these probabilities level off as we increase the maximum age of the mutation. This happens for two reasons. One is, as mentioned above, the vast majority of mutations simply go extinct within a few generations. So mutations most mutations that arose 50 generations likely did not make it to the present day. The other reason is that the human population was much smaller even just a few generations ago than it is today, so the average number of copies of each mutation introduced per generation was much smaller (e.g. about 200 million 50 generations ago, compared to the 7.6 billion figure of today).
Ok, so why is any of this relevant? On some level, I think it isn't terribly. The procedure is unethical for a whole host of reasons, many of which are covered in the links given at the top of this post. It does highlight however, that the natural/unnatural distinction that one might be tempted to make is not particular relevant here. Even when the mutations are assumed to have overwhelmingly negative deleterious consequences, they are reasonably likely to have arisen de novo somewhere in the world in someone alive today, and their probability of being present is only marginally impacted if we instead assume they are harmless.
1. Briefly, I downloaded numbers for the estimated total human population size in each year from the Our World in Data project. I then assumed that the current generation arose in 2015 (the last year for which the file I downloaded has data on population size), and that generation increments occur every 29 years. So, for example, this approximation assumes that there were 7.3 billion people all born in 2015, that they are descended from a population of about 4.9 billion people all born in 1986, who were in turn descended from a population of about 2.8 billion people all born in 1957, etc. Obviously, this is a bit silly, but averaged back over a few dozen generations, should actually approximated the rate at which mutations entered the population at different times in the recent past. In each generation, each copy of a mutation that is segregating is inherited by a Poisson number of offspring, with mean equal to the mutation's fitness effect. This process of mutation, selection and inheritance is iterated through the generations until the present day, at which point I simply check whether there is at least one copy of the mutation present in the population. I repeat this 10,000 times for each set of parameters, and the proportion of simulations in which at least one copy of the mutation is present gives our estimated probability.
2. I am, admittedly, making this assumption purely for modeling convenience. It's not really clear why one should think that mutations in CCR5, which codes for a protein presented on the surface of white blood cells, should impact fertility. More likely, because it is involved in immunity we might think that it would impact viability, as individuals carrying any of the mutations may be more or less susceptible to certain viruses besides HIV. However, this immediately make the problem much harder, as we would need to worry about the age structure of the present population (e.g. older individuals are more likely to have encountered a virus to which the mutation might leave them susceptible), etc. This is simply beyond the scope of what I can cover in a blog post, so my individual fertility selection assumption will have to do.
 RSS Feed
RSS Feed